1.
学习了平行四边形的知识后，同学们进行了拓展性研究．他们发现作平行四边形一组对角的角平分线与另一组对角的顶点所连对角线相交，则这两个交点与这条对角线两侧的对角顶点的连线所围成的封闭图形是一个特殊四边形．他们的解决思路是通过证明对应线段平行且相等得出结论．请根据以上思路完成下列作图和填空：
(1)
用直尺和圆规，过点B作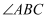
的角平分线，交AC于点F ， 连接BE、DF ． （只保留作图痕迹）
(2)
已知：如图，四边形ABCD是平行四边形，AC是对角线，DE平分
， 交AC于点E ， BF平分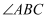 ， 交AC于点F ， 连接BE、DF ．
求证：四边形BEDF是平行四边形．
证明：∵四边形ABCD是平行四边形，
∴ ， ▲
∴ ．
∵DE平分 ， BF平分
，
∴ ．
∵
∴ ▲ ，
∴
∴ ▲ ， ．
∴﹐
∴四边形BEDF是平行四边形．
同学们再进一步研究发现，过平行四边形任意一组对角的顶点作平行线与另一组对角顶点所连对角线相交，均具有此特征．请你依照题意完成下面命题：
过平行四边形一组对角的顶点作平行线与另一组对角顶点所连对角线相交，则这两个交点与这条对角线两侧的对角顶点的连线所 ▲ ．
【考点】
平行四边形的判定与性质;
三角形全等的判定-ASA;
尺规作图-作角的平分线;
