1.
如图, 分别是
分别是 的高线、角平分线和中线.
的高线、角平分线和中线.

(1)
有下列结论:① ;②
;② ;③
;③ ;④
;④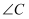 与
与 互余.其中正确的是_______(填序号).
(2)
若
互余.其中正确的是_______(填序号).
(2)
若 , 求
, 求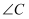 的度数.
的度数.
【考点】
余角、补角及其性质;
三角形内角和定理;
三角形的中线;
三角形的高;
三角形的角平分线;


