1.
已知 的直径
的直径 , 弦
, 弦 与弦
与弦 交于点
交于点 , 且
, 且 , 垂足为点F.
, 垂足为点F.

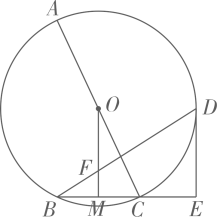
(1)
如图1,若 , 求线段
, 求线段 的长.
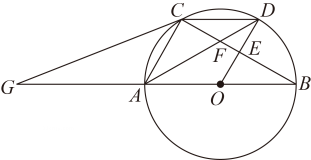
(2)
如图2,若
的长.
(2)
如图2,若 , 求
, 求 的正切值.
(3)
连结
的正切值.
(3)
连结 ,
,  ,
,  , 若
, 若 是
是 的内接正
的内接正 边形的一边,
边形的一边, 是
是 的内接正
的内接正 边形的一边,求
边形的一边,求 的面积.
的面积.
【考点】
勾股定理;
垂径定理;
圆周角定理;
解直角三角形;