1.
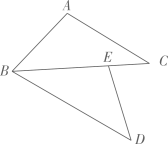
在等边△ABC的两边AB 、AC 所在直线上分别有两点M 、N,D 为△ABC外一点,且∠MDN=60°, ∠BDC=120°,BD=DC. 探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之 间的数量关系及△AMN的周长Q 与等边△ABC的周长L的关系。

(1)
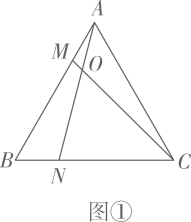
如图1,当点M、N 在边AB、AC 上,且DM=DN 时 ,BM、NC、MN之间的数量关系是 此时 = 。
(2)
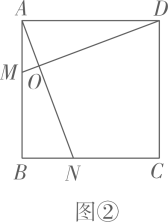
如图2,点M 、N 在边AB 、AC 上,且当DM≠DN 时,猜想(I) 问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由。
(3)
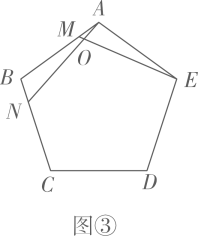
如图3,当M 、N 分别在边AB 、CA 的延长线上时,探索BM 、NC 、MN 之间的数量关系如何?并给出证明。
= 。
(2)
如图2,点M 、N 在边AB 、AC 上,且当DM≠DN 时,猜想(I) 问的两个结论还成立吗?若成立请直接写出你的结论;若不成立请说明理由。
(3)
如图3,当M 、N 分别在边AB 、CA 的延长线上时,探索BM 、NC 、MN 之间的数量关系如何?并给出证明。
【考点】
直角三角形全等的判定-HL;
三角形全等的判定-SAS;
能力提升
真题演练