1.
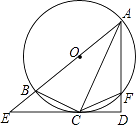
如图,AB , CD为⊙O的直径,点E在 上,连接AE , DE , 点G在BD的延长线上,AB=AG , ∠EAD+∠EDB=45°.
上,连接AE , DE , 点G在BD的延长线上,AB=AG , ∠EAD+∠EDB=45°.

(1)
求证:AG与⊙O相切;
(2)
若 ,
,  , 求DE的长.
, 求DE的长.
【考点】
圆周角定理;
切线的判定;
同角三角函数的关系;
等腰直角三角形;
已知正弦值求边长;