1.
折纸是富有趣味和有意义的一项活动，折纸中隐含着数学知识与思想方法．深入探究折纸，可以用数学的眼光发现，用数学的思维思考，用数学的语言描述，提升同学们的综合素养．
【操作发现】
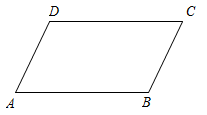
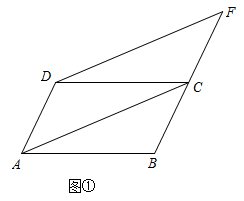
如图，一张菱形纸片ABCD，∠ABC=60°，AB=6cm，E，F分别为边AD，BC上的两个动点，小明将菱形纸片沿着EF翻折，得到四边形A'B'FE，点A，B的对应点分别为点A' ， B' ． 他发现了：点E从点A开始运动到点D结束的过程中，总能找到一个点F，使得点A' ， C，B'三点在同一直线上．
【操作发现】
如图，一张菱形纸片ABCD，∠ABC=60°，AB=6cm，E，F分别为边AD，BC上的两个动点，小明将菱形纸片沿着EF翻折，得到四边形A'B'FE，点A，B的对应点分别为点A' ， B' ． 他发现了：点E从点A开始运动到点D结束的过程中，总能找到一个点F，使得点A' ， C，B'三点在同一直线上．
【深入探究】
操作 | 探究内容 | 图形 |
操作一 | 当点E位于AD中点时，找到一个点F，将菱形纸片沿着EF翻折后，使得点D，A' ， C，B'四个点在同一直线上. |
|
操作二 | 将菱形纸片沿着EF翻折后，使得点A'，C，B'三点在同一直线上，且得到△B'CF是直角三角形. |
|
操作三 | 当 当点E位于AD靠近点D的三等分点时，找到一个点F，将菱形纸片沿着EF翻折后，使得点A'，C，B'三点在同一直线上，且A'E与CD交于点G. |
|
【解决问题】
(1)
根据操作一探究内容， 求证： 
；
(2)
根据操作二探究内容， 当 
为直角三角形时， 求 
的长度；
(3)
根据操作三探究内容， 直接写出 
的长度.
【考点】
直角三角形全等的判定-HL;
等边三角形的判定;
平行四边形的判定与性质;
菱形的性质;
三角形全等的判定-AAS;
