在直角坐标平面内，已知点A（a，0）在x轴负半轴上，点B（0，b）在y轴负半轴上，直线BC//x轴，点P为y轴上一点，射线PQ⊥AP交直线BC于点Q.

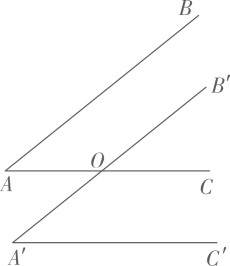
1. 在直角坐标平面内，已知点A（a，0）在x轴负半轴上，点B（0，b）在y轴负半轴上，直线BC//x轴，点P为y轴上一点，射线PQ⊥AP交直线BC于点Q.

(1) 点P在线段OB上时，试说明∠OAP=∠QPB的理由；

(2) 如果△BPQ是等腰三角形，求点Q的坐标；

(3) 如果以B、P、Q为顶点的三角形与△AOP全等，如存在，试直接写出点P的坐标；如不存在，试说明理由.

【考点】

垂线的概念; 平行线的性质; 三角形内角和定理; 等腰直角三角形; 数学思想;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，点A ， B分别为∠MON的边OM ， ON上的定点，点C为射线ON上的动点(不与点O ， B重合)．连接AC ，过点C作CD⊥AC ，过点B作BE∥OA ，交直线CD于点F ．

图1 图2

(1) 如图1，若点C在线段OB的延长线上，

①依题意补全图1；

②用等式表示∠OAC与∠BFC的数量关系，并说明理由；

(2) 如图2，若点C在线段OB上，直接用等式表示出∠OAC与∠BFC的数量关系．

综合题困难

2. 已知 $\text{[math]}$ 与 $\text{[math]}$ ，其中 $\text{[math]}$ 是锐角，设 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ ， $\text{[math]}$ 时，那么 $\text{[math]}$ 与 $\text{[math]}$ 有什么数量关系？

(1) 勤奋的小明同学，根据题意画出了下面图形，请根据小明的图形判断此时 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是；

(2) 善于思考的小颖同学认为小明同学的解答不够全面，缺少了一种情况 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系还可能是什么？请画出图形，并说明理由；

(3) 学霸小乐将原题中的条件 $\text{[math]}$ 改为 $\text{[math]}$ ，其它条件均不变，请直接写出此时 $\text{[math]}$ 与 $\text{[math]}$ 有什么数量关系．

综合题困难

3. 实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等，如图1，一束光线 $\text{[math]}$ 射到平面镜 $\text{[math]}$ 上，被 $\text{[math]}$ 反射后的光线为 $\text{[math]}$ ，则入射光线 $\text{[math]}$ ，反射光线 $\text{[math]}$ 与平面镜 $\text{[math]}$ 所夹的锐角 $\text{[math]}$ ．

(1) 如图2，一束光线 $\text{[math]}$ 射到平面镜 $\text{[math]}$ 上，被 $\text{[math]}$ 反射到平面镜 $\text{[math]}$ 上，又被 $\text{[math]}$ 反射，若被 $\text{[math]}$ 反射出的光线 $\text{[math]}$ 与光线 $\text{[math]}$ 平行，且 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ；

(2) 图2中，当被 $\text{[math]}$ 反射出的光线 $\text{[math]}$ 与光线 $\text{[math]}$ 平行时，不论 $\text{[math]}$ 如何变化， $\text{[math]}$ 与 $\text{[math]}$ 总具有一定的数量关系，请你探究 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并说明理由；

(3) 图2中，由（1）、（2），请你探究：当任何射到平面镜 $\text{[math]}$ 上的光线 $\text{[math]}$ ，经过平面镜 $\text{[math]}$ 、 $\text{[math]}$ 的两次反射后，入射光线 $\text{[math]}$ 与反射光线 $\text{[math]}$ 平行，求两平面镜 $\text{[math]}$ 、 $\text{[math]}$ 的夹角 $\text{[math]}$ 的度数，并说明理由．

(4) 如图3，一束光线 $\text{[math]}$ 射到平面镜 $\text{[math]}$ 上，被 $\text{[math]}$ 反射到平面镜 $\text{[math]}$ 上，又被 $\text{[math]}$ 反射，若被 $\text{[math]}$ 反射出的光线 $\text{[math]}$ 与光线 $\text{[math]}$ 垂直，则 $\text{[math]}$ 等于多少度？（友情提示：三角形内角和等于 $\text{[math]}$ ）

综合题困难