1.
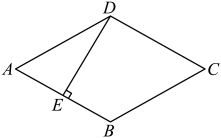
如图1,在菱形四边形 中,E、F分别是边
中,E、F分别是边 上的动点,且
上的动点,且 , 连接
, 连接 交
交 于点O .
于点O .

(1)
若 , 当点E运动到
, 当点E运动到 中点时,求
中点时,求 的度数;
(2)
如图2,在边
的度数;
(2)
如图2,在边 上取点M、N(点M在
上取点M、N(点M在 之间),使得
之间),使得 , 点P是
, 点P是 上的动点.若点E从点A匀速运动到点D时,点P恰好从点M匀速运动到点N , 设
上的动点.若点E从点A匀速运动到点D时,点P恰好从点M匀速运动到点N , 设 , 已知
, 已知 , 请分别求出
, 请分别求出 的长;
(3)
如图3,在(2)的条件下,连接
的长;
(3)
如图3,在(2)的条件下,连接 , 若
, 若 , 求
, 求 面积的最大值.
面积的最大值.
【考点】
二次函数的最值;
菱形的性质;
四边形-动点问题;
解直角三角形—边角关系;