组卷在线网-ZUJUAN.COM

1.

(1) 问题情境：

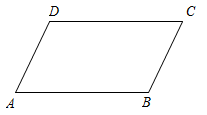
数学活动课上，小明向同学们提出了这样一个问题：如图（1），在矩形 $\text{[math]}$ 中， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，作射线 $\text{[math]}$ ，连接 $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系；

(2) 解决问题：

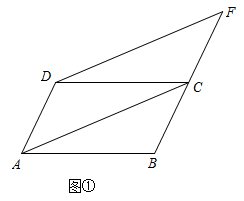
小亮受此问题启发，将矩形 $\text{[math]}$ 变为平行四边形，其中 $\text{[math]}$ 为锐角，如图（2）， $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，过点 $\text{[math]}$ 作 $\text{[math]}$ 交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，交射线 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ ，请你证明小亮的结论；

(3) 拓展探究：

小宇在小亮结论的基础上进行了探究，并提出了一个新问题： $\text{[math]}$ 与 $\text{[math]}$ 有怎样的数量关系？请你回答小宇提出的这个问题，并证明你的结论．

【考点】

线段垂直平分线的性质; 等腰三角形的性质; 平行四边形的判定与性质; 矩形的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 【教材呈现】下图是华师版八年级下册数学教材第83页和84页的部分内容．

平行四边形的判定定理2 一组对边平行且相等的四边形是平行四边形．

我们可以用演绎推理证明这一结论．

已知：如图，在四边形 $\text{[math]}$ 中，AB $\text{[math]}$ CD且 $\text{[math]}$ ．

求证：四边形 $\text{[math]}$ 是平行四边形．

证明：连接 $\text{[math]}$ ．

(1) 请根据教材提示，结合图，写出完整的证明过程．

(2) 【知识应用】如图①，在 $\text{[math]}$ 中，延长 $\text{[math]}$ 到点 $\text{[math]}$ ，使 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ ．求证：四边形 $\text{[math]}$ 是平行四边形．

(3) 【拓展提升】在【知识应用】的条件下，若四边形 $\text{[math]}$ 的面积为7，直接写出四边形 $\text{[math]}$ 的面积．

实践探究题普通