0 返回首页
1. 在矩形ABCD中，AB＝3，BC＝2，以点A为旋转中心，按逆时针方向旋转矩形ABCD ， 旋转角为α（0°＜α＜180°），得到矩形AEFG ， 点B、点C、点D的对应点分别为点E、点F、点G ．

(1) 如图①，当点E落在DC边上时，线段EC的长度为 ．
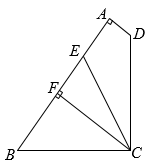
(2) 如图②，连结CF ， 当点E落在线段CF上时，AE与DC相交于点H ， 连结AC ，

①求证：△ACD≌△CAE ．

②线段DH的长度为  ▲  ．

(3) 如图③，设点P为边GF的中点，连结PB、PE、BE ， 在矩形ABCD旋转的过程中，△BEP面积的最大值为．
【考点】
三角形的面积; 三角形全等及其性质; 直角三角形全等的判定-HL; 勾股定理; 矩形的性质; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
换一批
1. 如图①，有一组平行线l1∥l2∥l3∥l4 ， 正方形ABCD的四个顶点分别在l1、l2、l3、l4上，EG过点D且垂直于l1于点E，分别交l2、l4于点F、G，EF＝DG＝1，DF＝2.

(1) AE＝，正方形ABCD的边长＝；
(2) 如图②，将∠AED绕点A顺时针旋转α°得到∠AE′D′，且0°＜α＜90°，点D′在直线l3上，以AD′为边在E′D′左侧作菱形AD′C′B′，使点B′、C′分别在直线l2、l4上．

①写出∠B′AD′与α的函数关系并给出证明；

②若α＝30°，求菱形AD′C′B′的边长．
综合题 困难
2. 如图，在每个小正方形的边长均为1的方格纸中有线段AB和CD，点A、B、C、D均在小正方形的顶点上．

(1) 画出一个以AB为一边的△ABE，点E在小正方形的顶点上，且∠BAE＝45°，△ABE的面积为；
(2) 画出以CD为一腰的等腰△CDF，点F在小正方形的顶点上，且△CDF的面积为；
(3) 在（1）、（2）的条件下，连接EF，请直接写出线段EF的长．
综合题 普通
3. 如图，在四边形ABCD中， ， CF∥AD， ， ， E是AF的中点，CE平分 ．

(1) 求证：；
(2) 若 ， 求 ．
综合题 普通