1.
如图1,在平面直角坐标系中,直线AB分别交y轴、x轴于点A(0,a),点B(b,0),且a、b满足a2-4a+4+ =0.
=0.
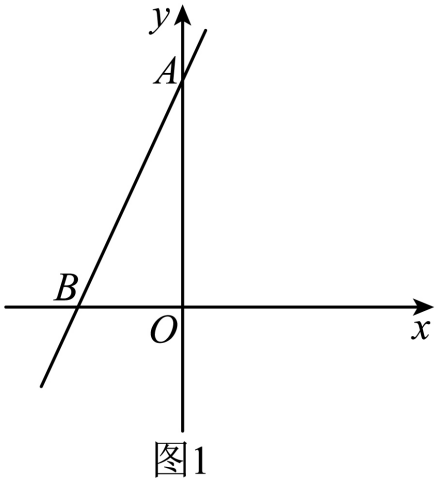
(1)
求a,b的值;
(2)
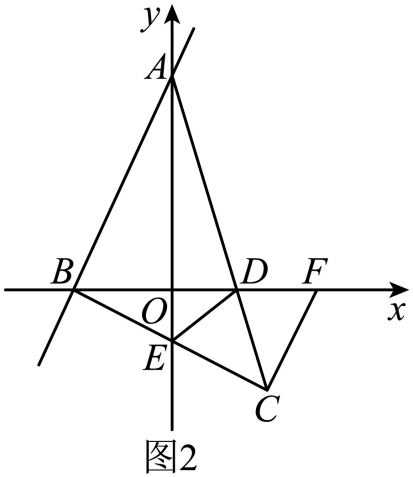
以AB为边作Rt△ABC,点C在直线AB的右侧,且∠ACB=45°,求点C的坐标;
(3)
若(2)的点C在第四象限(如图2),AC与 x轴交于点D,BC与y轴交于点E,连接 DE,过点C作CF⊥BC交x轴于点F.
①求证:CF=BC;
②直接写出点C到DE的距离.
【考点】
偶次方的非负性;
算术平方根的性质(双重非负性);
三角形全等的判定-SAS;
三角形全等的判定-ASA;
三角形全等的判定-AAS;
能力提升