1.
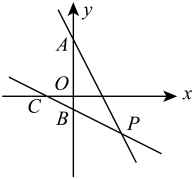
如图①,在平面直角坐标系中有一个 , 点
, 点 两点在坐标轴上,其中
两点在坐标轴上,其中 ,
,  ,
,  , 将该三角形沿直线
, 将该三角形沿直线 翻折得到
翻折得到 .
.

(1)
点 的坐标为,点
的坐标为,点 的坐标为,
的坐标为, 边所在直线的函数表达式为.
(2)
在图①中,一动点P从点O出发,沿折
边所在直线的函数表达式为.
(2)
在图①中,一动点P从点O出发,沿折 的方向,以每秒2个单位长度的速度向点
的方向,以每秒2个单位长度的速度向点 运动,设运动时间为
运动,设运动时间为 秒.请求出
秒.请求出 的面积
的面积 与
与 之间的函数关系,并求出当
之间的函数关系,并求出当 为何值时,
为何值时, 的面积为
的面积为 面积的
面积的 .
(3)
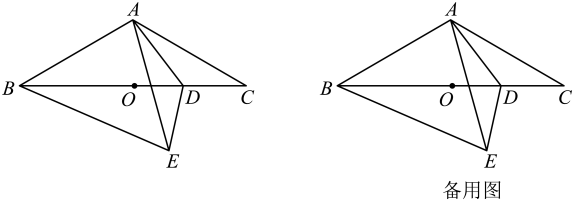
如图②,固定
.
(3)
如图②,固定 , 将
, 将 绕点
绕点 逆时针旋转,旋转后得到
逆时针旋转,旋转后得到 , 设
, 设 所在直线与
所在直线与 所在直线的交点为点
所在直线的交点为点 . 请问在旋转过程中是否存在点
. 请问在旋转过程中是否存在点 , 使
, 使 为等腰三角形?若存在,请写出点
为等腰三角形?若存在,请写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【考点】
一次函数图象与几何变换;
翻折变换(折叠问题);
一次函数中的动态几何问题;
能力提升