1.
综合与探究
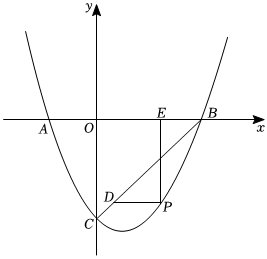
如图,已知抛物线 与
与 轴交于
轴交于 ,
,  两点
两点 点
点 位于点
位于点 的右边
的右边 , 与
, 与 轴交于点
轴交于点 , 连接
, 连接 ,
,  是抛物线上的一动点,点
是抛物线上的一动点,点 的横坐标为
的横坐标为 .
.
如图,已知抛物线

(1)
求 ,
,  两点的坐标.
(2)
若
两点的坐标.
(2)
若 , 点
, 点 位于第四象限,过点
位于第四象限,过点 作
作 轴的平行线交
轴的平行线交 于点
于点 , 过点
, 过点 作
作 轴的平行线交
轴的平行线交 轴于点
轴于点 , 求
, 求 的最大值及此时点
的最大值及此时点 的坐标.
(3)
在
的坐标.
(3)
在 中
中 取得最大值的条件下,将该抛物线沿水平方向向左平移
取得最大值的条件下,将该抛物线沿水平方向向左平移 个单位长度,
个单位长度, 为点
为点 的对应点,平移后的抛物线与
的对应点,平移后的抛物线与 轴交于点
轴交于点 ,
,  为平移后的抛物线的对称轴上一点
为平移后的抛物线的对称轴上一点 在平移后的抛物线上确定一点
在平移后的抛物线上确定一点 , 使得以
, 使得以 ,
,  ,
,  ,
,  为顶点的四边形是平行四边形,直接写出所有符合条件的点
为顶点的四边形是平行四边形,直接写出所有符合条件的点 的坐标.
的坐标.
【考点】
待定系数法求一次函数解析式;
二次函数图象的几何变换;
二次函数图象与坐标轴的交点问题;
平行四边形的性质;
二次函数图象上点的坐标特征;