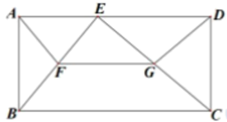
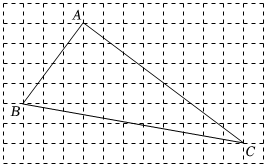
如图，正方形网格中的每个小正方形的边长都是，点、、均在格点上．

1. 如图，正方形网格中的每个小正方形的边长都是 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 均在格点上．

(1) 图中线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；

(2) 求证： $\text{[math]}$ 是直角三角形．

【考点】

勾股定理; 勾股定理的逆定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

作图题普通

1. 如图，在4x3正方形网格中，每个小正方形的边长都是1．

(1) 分别求出线段AB、CD的长度；

(2) 在图中画出线段EF、使得EF的长为 $\text{[math]}$ ，以AB、CD、EF三条线段能否构成直角三角形，并说明理由.

作图题普通

2. 如图，在正方形网格中，每个小正方形的边长都是 1.

(1) 填空： $\text{[math]}$ ， $\text{[math]}$ ； $\text{[math]}$

(2) 在图中画出一条线段 $\text{[math]}$ ，使得 $\text{[math]}$ ；判断以 $\text{[math]}$ 三条线段为边能否构成直角三角形？请说明理由.

作图题普通

3. 如图，在 $\text{[math]}$ 的方格纸中，每个小正方形的边长都为 $\text{[math]}$ 的三个顶点都在格点上，已知 $\text{[math]}$ ， $\text{[math]}$ .

(1) 画出 $\text{[math]}$ ；

(2) 判断 $\text{[math]}$ 的形状，并说明理由.

作图题普通