已知，如图，等腰△ABC ， AC＝BC ， CN平分∠ACM ．

1. 已知，如图，等腰△ABC ， AC＝BC ， CN平分∠ACM ．

(1) 如图1，求证：CN∥AB；

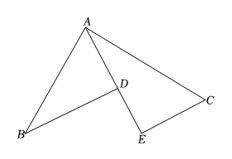
(2) 如图2，若△ABC是等边三角形，在BC上取点D ， CN上取点E ，使BD＝CE ，连接AD ， DE ， AE ．求证：△ADE是等边三角形；

(3) 如图3，在（2）的条件下，过B点作BH∥DE ，分别交AD ， AC ， AE于G ， F ， H ，连接HC交DE于点K ，若HK：KC＝1：2，GF＝4，AE＝7，求DG的长．

【考点】

三角形全等及其性质; 等边三角形的判定与性质; 同位角相等，两直线平行; 两直线平行，同位角相等; 等腰三角形的性质-等边对等角;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. △ABC和△ADE都是等边三角形．

(1) 将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P(点P与点A重合)，有PA+PB=PC(或PA+ PC= PB)成立(不需证明)；
将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P ，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；

(2) 将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明．

综合题普通

2. 如图所示，已知 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ≌ $\text{[math]}$ ．

(1) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

(2) 求证： $\text{[math]}$ ．

综合题普通

3. 如图， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点在同一条直线上，且 $\text{[math]}$ ≌ $\text{[math]}$ ．

(1) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ ．

综合题普通