1.
(1)
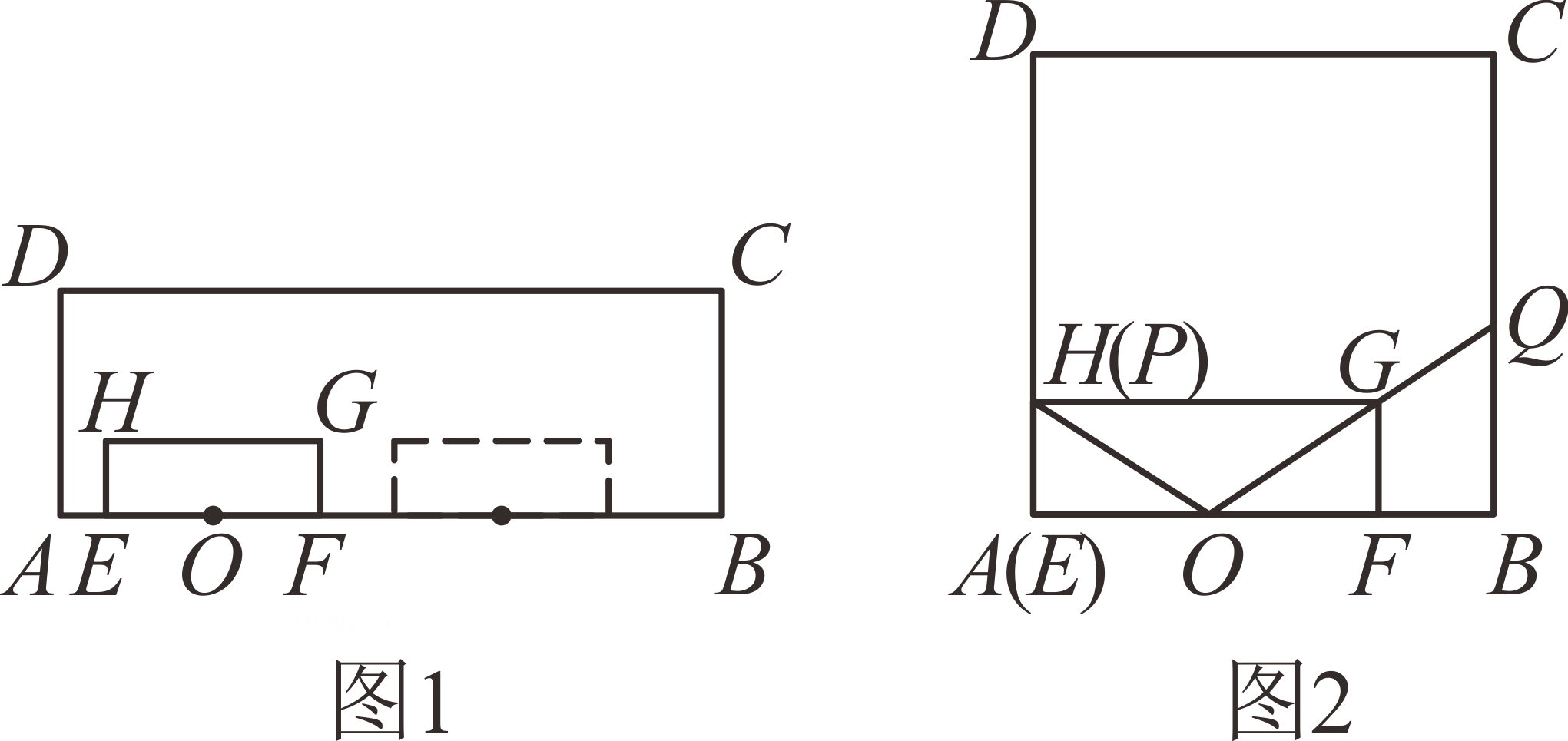
【问题提出】如图1，在四边形
中，
， 点
是
上一点，连接
、
， 若
， 求证：
；
(2)
【问题探究】如图2，在
中，
， 点是上一点，过点作
交
于点
， 若
， 
， 
， 求
的值；
(3)
【问题解决】如图3，四边形
是某公园的一块空地，
， 分别沿
、
修两条小路，并在
区域内栽种竹子，其余部分进行绿化，已知
， 
， 
， 求栽种竹子的面积（即的面积）．
【考点】
三角形的面积;
勾股定理;
相似三角形的判定与性质;
锐角三角函数的定义;
