已知，△ABC中，AB＝AC ，过点A作AE∥BC ， ∠CAE＝60°．

1. 已知，△ABC中，AB＝AC ，过点A作AE∥BC ， ∠CAE＝60°．

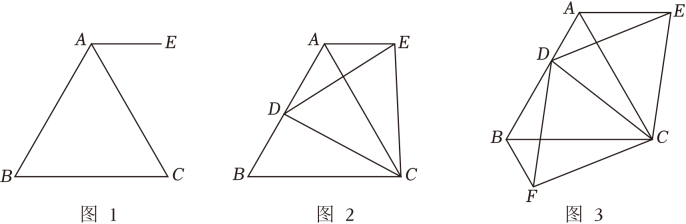
(1) 如图1，求证：△ABC是等边三角形；

(2) 如图2，点D是边AB上一动点（点D与点A、B不重合），连接DC、DE、CE ，若∠DEC＝60°，求证：BC＝AE+AD；

(3) 如图3，在（2）的条件下，作△DCE关于直线CD对称的△DCF ，连接BF ，若AE＝ $\text{[math]}$ BF ， CB＝8，求BD的长．

【考点】

平行线的性质; 等边三角形的判定与性质; 轴对称的性质; 一元一次方程的实际应用-几何问题; 三角形全等的判定-SAS; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 问题情境：综合实践课上，王老师组织同学们开展了探究三角之间数量关系的数学活动．

(1) 如图1， $\text{[math]}$ ，点 $\text{[math]}$ 分别为直线 $\text{[math]}$ 上的一点，点 $\text{[math]}$ 为平行线间一点且 $\text{[math]}$ ，求 $\text{[math]}$ 度数；

问题迁移：

(2) 如图2，射线 $\text{[math]}$ 与射线 $\text{[math]}$ 交于点 $\text{[math]}$ ，直线 $\text{[math]}$ ，直线 $\text{[math]}$ 分别交 $\text{[math]}$ 于点 $\text{[math]}$ ，直线 $\text{[math]}$ 分别交 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 在射线 $\text{[math]}$ 上运动．①当点 $\text{[math]}$ 在 $\text{[math]}$ （不与 $\text{[math]}$ 重合）两点之间运动时，设 $\text{[math]}$ ．则 $\text{[math]}$ 之间有何数量关系？②若点 $\text{[math]}$ 不在线段 $\text{[math]}$ 上运动时（点 $\text{[math]}$ 与点 $\text{[math]}$ 三点都不重合），请你直接写出 $\text{[math]}$ 间的数量关系．

解答题普通

2. 如图，在△ABC中，∠BAC=90°， $\text{[math]}$ 平分∠ABC， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，已知∠D=29°，求∠1的度数.

解答题普通

3. 如图， $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的度数.

解答题普通