1.
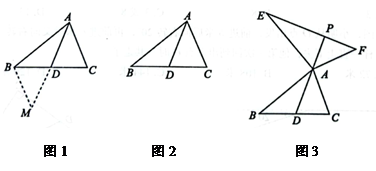
为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽在组内做了如下尝试:如图1,在 中,
中, 是
是 边上的中线,延长
边上的中线,延长 到
到 , 使
, 使 , 连接
, 连接 .
.
(1)
【探究发现】图1中 与
与 的数量关系是,位置关系是;
(2)
【初步应用】如图2,在
的数量关系是,位置关系是;
(2)
【初步应用】如图2,在 中,若
中,若 , 求
, 求 边上的中线
边上的中线 的取值范围;
(3)
【探究提升】如图3,
的取值范围;
(3)
【探究提升】如图3, 是
是 的中线,过点
的中线,过点 分别向外作
分别向外作 , 使得
, 使得 , 延长
, 延长 交
交 于点
于点 , 判断线段
, 判断线段 与
与 的数量关系和位置关系,请说明理由.
的数量关系和位置关系,请说明理由.
【考点】
三角形的角平分线、中线和高;
三角形三边关系;
三角形全等及其性质;
三角形全等的判定-SAS;
三角形的综合;
能力提升