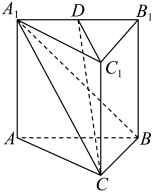
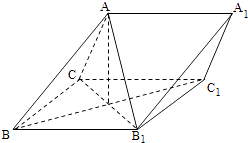
如图所示的多面体中，底面ABCD为矩形，平面ABCD ，平面ABCD ，平面ABCD ，，且AB=4，BC=2，， BE=1．

1. 如图所示的多面体中，底面ABCD为矩形， $\text{[math]}$ 平面ABCD ， $\text{[math]}$ 平面ABCD ， $\text{[math]}$ 平面ABCD ， $\text{[math]}$ ，且AB=4，BC=2， $\text{[math]}$ ， BE=1．

(1) 求BF的长；

(2) 求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 成的角的正弦值．

【考点】

空间向量的夹角与距离求解公式; 用空间向量研究二面角;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图所示，半圆柱的轴截面为平面 $\text{[math]}$ ， $\text{[math]}$ 是圆柱底面的直径， $\text{[math]}$ 为底面圆心， $\text{[math]}$ 为一条母线， $\text{[math]}$ 为 $\text{[math]}$ 的中点，且 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 夹角的余弦值.

解答题普通

2. 如图四棱锥 $\text{[math]}$ ，且 $\text{[math]}$ ，平面 $\text{[math]}$ 平面 $\text{[math]}$ ，且 $\text{[math]}$ 是以 $\text{[math]}$ 为直角的等腰直角三角形，其中 $\text{[math]}$ 为棱 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在棱 $\text{[math]}$ 上，且 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ 四点共面；

(2) 求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 夹角的余弦值.

解答题普通

3. 如图，在直三棱柱 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，且二面角为 $\text{[math]}$ 为45°.

(1) 求棱AC的长；

(2) 若D为棱 $\text{[math]}$ 的中点，求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 夹角的正切值.

解答题普通