1.
我国南宋时期数学家秦九韶（约1202﹣约1261）曾提出利用三角形的三边求面积的秦九韶公式：如果一个三角形的三边长分别为a ， b ， c ， 记p＝
， 那么三角形的面积S＝
． 在△ABC中，已知BC＝5，AC＝6，AB＝7．
(1)
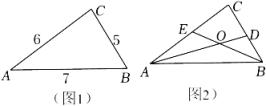
如图1，利用秦九韶公式求△ABC的面积；
(2)
如图2，△ABC的两条角平分线AD ， BE交于点O ， 求点O到边AB的距离．
【考点】
三角形的面积;
角平分线的性质;
几何图形的面积计算-割补法;
