1.
如图1,四边形ABCD是正方形,E,F分别在边BC和CD上,且∠EAF=45°,我们把这种模型称为“半角模型”,在解决“半角模型”问题时,旋转是一种常用的方法。小明为了解决线段EF,BE,DF之间的关系,将△ADF绕点A顺时针旋转90°后解决了这个问题。
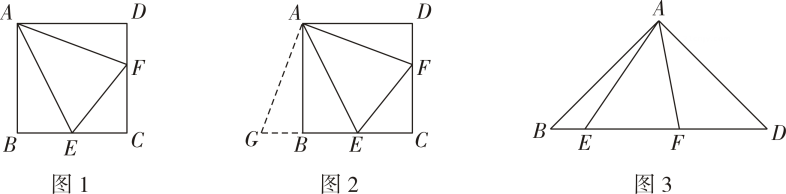
(1)
请直接写出线段EF,BE,DF之间的关系.
(2)
如图3,等腰直角三角形ABD,∠BAD=90°,AB=AD,点E,F在边BD上,且∠EAF=45°,请写出EF,BE,DF之间的关系,并说明理由.
【考点】
勾股定理;
正方形的性质;
旋转的性质;
等腰直角三角形;
三角形全等的判定-SAS;


