已知，正六边形ABCDEF ，边长为6，G点以每秒为1的速度从A→B→C→D→E上运动，不与E点重合，同时，点H以同样的速度从B→C→D→E→F上运动，不与F点重合，连接GF、AH交于点I；

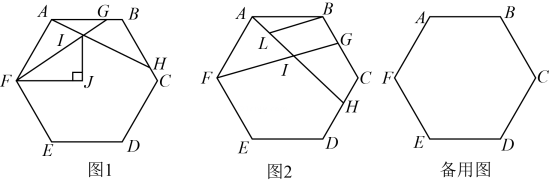
1. 已知，正六边形ABCDEF ，边长为6，G点以每秒为1的速度从A→B→C→D→E上运动，不与E点重合，同时，点H以同样的速度从B→C→D→E→F上运动，不与F点重合，连接GF、AH交于点I；

(1) 求∠E的度数．

(2) 如图1，IJ是∠FIH的角平分线，过F点作IJ的垂线，垂足为J ，当FI是∠AFJ的角平分线时，求证AI＝IJ ．

(3) 如图2，过B点作FG的平行线，交直线AH于点L ，当G在运动的过程中，写出FI、AL、AI之间的数量关系，并给出证明．

【考点】

三角形全等及其性质; 角平分线的性质; 等边三角形的判定与性质; 正多边形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. △ABC和△ADE都是等边三角形．

(1) 将△ADE绕点A旋转到图①的位置时，连接BD，CE并延长相交于点P(点P与点A重合)，有PA+PB=PC(或PA+ PC= PB)成立(不需证明)；
将△ADE绕点A旋转到图②的位置时，连接BD，CE相交于点P ，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明；

(2) 将△ADE绕点A旋转到图③的位置时，连接BD，CE相交于点P，连接PA，猜想线段PA、PB、PC之间有怎样的数量关系？并加以证明．

综合题普通

2. 如图所示，已知 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ ≌ $\text{[math]}$ ．

(1) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

(2) 求证： $\text{[math]}$ ．

综合题普通

3. 如图， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点在同一条直线上，且 $\text{[math]}$ ≌ $\text{[math]}$ ．

(1) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ ．

综合题普通