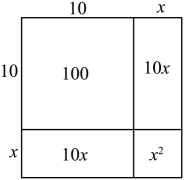
下面是小李同学探索的近似数的过程：面积为107的正方形边长是，且，设，其中，画出如图示意图，因为图中，，所以当较小时，省略，得，得到，即．

1. 下面是小李同学探索 $\text{[math]}$ 的近似数的过程：

$\text{[math]}$ 面积为107的正方形边长是 $\text{[math]}$ ，且 $\text{[math]}$ ，

$\text{[math]}$ 设 $\text{[math]}$ ，其中 $\text{[math]}$ ，画出如图示意图，

因为图中 $\text{[math]}$ ， $\text{[math]}$ ，

所以 $\text{[math]}$

当 $\text{[math]}$ 较小时，省略 $\text{[math]}$ ，得 $\text{[math]}$ ，得到 $\text{[math]}$ ，即 $\text{[math]}$ ．

(1) $\text{[math]}$ 的整数部分是；

(2) 仿照上述方法，探究 $\text{[math]}$ 的近似值．（画出示意图，标明数据，并写出求解过程）

【考点】

无理数的估值;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题普通

1. 中国古代的数理天文学通常都是以分数的形式选择历法中用到的天文学常数.由于这些天文学常数基本上都是无理数，因此，历法家们设计了一些算法用来挑选合适的有理数去逼近这些常数，这样的方法在数学上被称作“实数的有理逼近”.我国南北朝时期数学家何承天发明的“调日法”便是利用分数的加成性质而设计的一种实数的有理逼近算法，其步骤大体如下：设实数x的不足近似值和过剩近似值分别为 $\text{[math]}$ 和 $\text{[math]}$ （即有 $\text{[math]}$ ＜x＜ $\text{[math]}$ ，其中a，b，c，d为正整数），则 $\text{[math]}$ 是x的更为精确的近似值.例如：已知 $\text{[math]}$ ，则利用一次“调日法”后可得到π的一个更为精确的近似分数为 $\text{[math]}$ ；由于 $\text{[math]}$ ≈3.1404＜π，再由 $\text{[math]}$ $\text{[math]}$ ，可以再次使用“调日法”得到π的更为精确的近似分数 $\text{[math]}$ .

(1) 现已知 $\text{[math]}$ ，

使用一次“调日法”计算 $\text{[math]}$ 的一个更为精确的近似分数为；

使用二次“调日法”计算 $\text{[math]}$ 的一个更为精确的近似分数为；

使用三次“调日法”计算 $\text{[math]}$ 的一个更为精确的近似分数为；

(2) $\text{[math]}$ 的整数部分为x，小数部分为y，求x+2y的值.

实践探究题困难