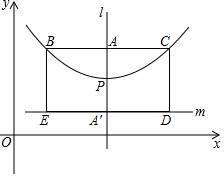
如图，在顶点为P的抛物线y＝a（x-h）2+k（a≠0）的对称轴l上取点A（h ， k+），过A作BC⊥l交抛物线于B、C两点（B在C的左侧），点A′和点A关于点P对称；过A′作直线m⊥l ，又分别过点B、C作BE⊥m和CD⊥m ，垂足为E、D ．在这里我们把点A叫此抛物线的焦点，BC叫此抛物线的直径，矩形BCDE叫此抛物线的焦点矩形．

1. 如图，在顶点为P的抛物线y＝a（x-h）²+k（a≠0）的对称轴l上取点A（h ， k+ $\text{[math]}$ ），过A作BC⊥l交抛物线于B、C两点（B在C的左侧），点A′和点A关于点P对称；过A′作直线m⊥l ，又分别过点B、C作BE⊥m和CD⊥m ，垂足为E、D ．在这里我们把点A叫此抛物线的焦点，BC叫此抛物线的直径，矩形BCDE叫此抛物线的焦点矩形．

(1) 直接写出抛物线y＝ $\text{[math]}$ x²的焦点坐标以及直径的长．

(2) 求抛物线y＝ $\text{[math]}$ （x-3）²+2的焦点坐标以及直径的长．

(3) 已知抛物线y＝a（x-h）²+k（a≠0）的直径为 $\text{[math]}$ ，求a的值．

(4) ①已知抛物线y＝ax²+bx+c（a≠0）的焦点矩形的面积为2，求a的值．

②直接写出抛物线y＝ $\text{[math]}$ （x-3）²+2的焦点矩形与抛物线y＝x²-2mx+m²+1有两个公共点时m的取值范围．

【考点】

矩形的性质; 图形的旋转; 中心对称及中心对称图形; 二次函数y=a（x-h）²+k的图象; 二次函数y=a（x-h）²+k的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 综合与实践

如图1，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，动点 $\text{[math]}$ 分别以 $\text{[math]}$ 的速度从点 $\text{[math]}$ 同时出发，点 $\text{[math]}$ 沿着 $\text{[math]}$ 运动到点 $\text{[math]}$ 时停止，点 $\text{[math]}$ 沿着 $\text{[math]}$ 运动到点 $\text{[math]}$ 时停止．设运动时间为 $\text{[math]}$ ．

(1) 当点 $\text{[math]}$ 在 $\text{[math]}$ 上运动时， $\text{[math]}$ ____________ $\text{[math]}$ ____________ $\text{[math]}$ ．（用含 $\text{[math]}$ 的代数式表示）

(2) 在（1）的条件下，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．

(3) 如图2、图3，点 $\text{[math]}$ 沿着 $\text{[math]}$ 运动到点 $\text{[math]}$ 的过程中，当 $\text{[math]}$ 的面积为 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．

解答题普通

2. 如图在平面直角坐标系中，O是坐标原点，矩形OACB的顶点A，B分别在x轴、y轴上，已知 $\text{[math]}$ ，点D为y轴上一点，其坐标为 $\text{[math]}$ ，若连接CD，则 $\text{[math]}$ ，点P从点A出发以每秒1个单位的速度沿线段 $\text{[math]}$ 的方向运动，当点P与点B重合时停止运动，运动时间为t秒

（1）求B，C两点坐标；

（2）求 $\text{[math]}$ 的面积S关于t的函数关系式；

（3）当点D关于OP的对称点E落在x轴上时，请直接写出点E的坐标，并求出此时的t值．

解答题普通

3. 如图，在矩形 $\text{[math]}$ 中， $\text{[math]}$ ，点P从点A沿 $\text{[math]}$ 向点B以 $\text{[math]}$ 的速度移动，同时点Q从点B沿 $\text{[math]}$ 边向点C以 $\text{[math]}$ 的速度移动．当其中一点达到终点时，另一点也随之停止．设P，Q两点移动的时间为 $\text{[math]}$ ，求：

(1) 当x为何值时， $\text{[math]}$ 为等腰三角形；

(2) 当x为何值时， $\text{[math]}$ 的面积为 $\text{[math]}$ ；

(3) 当x为何值时， $\text{[math]}$ 为等腰三角形．

解答题困难