1.
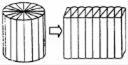
探索与发现。为了探究圆柱的体积,课堂上陈宣和本组同学一起进行了以下操作活动。

(1)
建立联系:拼成的长方体与原来的圆柱有什么联系?(至少写出两条)
(2)
归纳结论:整个推导过程运用了的思想方法。通过以上操作,你得出的结论是:圆柱的体积=。
(3)
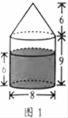
巧妙应用:下图是一根圆木沿一平面截去一部分后的剩余部分,请你计算剩余部分的体积。(单位:cm)

【考点】
圆柱的体积(容积);
能力提升
真题演练