1.
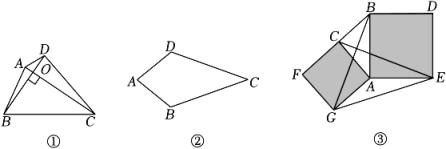
如图①,对角线互相垂直的四边形叫做垂美四边形.
(1)
【概念理解】如图②,在四边形ABCD中,AB=AD , CB=CD , 问四边形ABCD是垂美四边形吗?请说明理由;
(2)
【性质探究】如图①,四边形ABCD的对角线AC , BD交于点O , AC⊥BD . 试证明:AD2+BC2=AB2+CD2;
(3)
【解决问题】如图③,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE , 连接CE , BG , GE . 已知AC=8,AB=10,求GE的长.
【考点】
三角形全等及其性质;
线段垂直平分线的性质;
勾股定理;