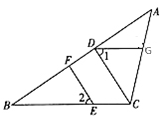
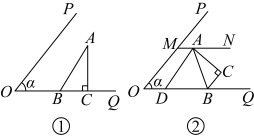
将一块三角板（，）按如图①所示放置在锐角内，使直角边落在边上，记，现将三角板绕点B逆时针以每秒的速度旋转t秒（直角边旋转到如图②所示的位置，且点A始终在内），过点A作交射线于点M，平分交射线于点D ，其中m的值满足使代数式取得最小值．

1. 将一块三角板 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）按如图①所示放置在锐角 $\text{[math]}$ 内，使直角边 $\text{[math]}$ 落在 $\text{[math]}$ 边上，记 $\text{[math]}$ ，现将三角板 $\text{[math]}$ 绕点B逆时针以每秒 $\text{[math]}$ 的速度旋转t秒（直角边 $\text{[math]}$ 旋转到如图②所示的位置，且点A始终在 $\text{[math]}$ 内），过点A作 $\text{[math]}$ 交射线 $\text{[math]}$ 于点M， $\text{[math]}$ 平分 $\text{[math]}$ 交射线 $\text{[math]}$ 于点D ，其中m的值满足使代数式 $\text{[math]}$ 取得最小值．

(1) m的值为；

(2) 当 $\text{[math]}$ 秒时，求 $\text{[math]}$ 的度数；

(3) 在某一时刻，当 $\text{[math]}$ 时，试探求 $\text{[math]}$ 与 $\text{[math]}$ 之间的数量关系．

【考点】

平行线的性质; 三角形内角和定理; 实数的绝对值; 角平分线的概念;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知直线 $\text{[math]}$ ，点 $\text{[math]}$ 在直线MN上，点B、C为平面内两点， $\text{[math]}$ 于点 $\text{[math]}$ .

(1) 如图1，当点 $\text{[math]}$ 在直线MN上，点 $\text{[math]}$ 在直线MN上方时，CB交PQ于点 $\text{[math]}$ ，求证： $\text{[math]}$ ；

(2) 如图2，当点 $\text{[math]}$ 在直线MN上且在点 $\text{[math]}$ 左侧，点 $\text{[math]}$ 在直线MN与PQ之间的，过点 $\text{[math]}$ 作 $\text{[math]}$ 交直线PQ于点 $\text{[math]}$ ，请猜测 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系，并说明理由；

(3) 如图3，当点 $\text{[math]}$ 在直线MN上，且在点 $\text{[math]}$ 左侧，点 $\text{[math]}$ 在直线PQ下方时，过点 $\text{[math]}$ 作 $\text{[math]}$ 交直线PQ于点 $\text{[math]}$ ，作 $\text{[math]}$ 的平分线交直线MN于点 $\text{[math]}$ ，当 $\text{[math]}$ $\text{[math]}$ 时，求出 $\text{[math]}$ 的度数.

综合题困难

2. 如图，政府规划由西向东修一条公路.从A修至B后为了绕开村庄，改为沿南偏东25°方向修建BC段，在C处又改变方向修建CD段，测得∠BCD＝70°，在D处继续改变方向，朝与出发时相同的方向修至E.

(1) 补全施工路线示意图，求∠CDE的度数；

(2) 原计划在AB的延长线上依次修建两个公交站M，N（均在CD右侧），连结DM和MN，求∠CDM与∠DMN的数量关系.

综合题普通

3. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F.

(1) CD与EF平行吗？为什么？

(2) 如果∠1＝∠2，试判断DG与BC的位置关系，并说明理由.

综合题普通