组卷在线网-ZUJUAN.COM

1.

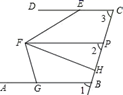
(1) 已知AB∥CD，点M为平面内一点.如图①，BM⊥CM，小颖说过点M作MP∥AB，很容易说明∠ABM和∠DCM互余.请你帮小颖写出具体的证明过程.

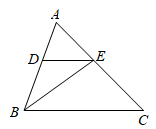
(2) 如图②，AB∥CD，点M在射线ED上运动，当点M移动到点A与点D之间时，试判断∠BMC与∠ABM，∠DCM的数量关系，并说明理由.

(3) 在(2)的条件下，当点M在射线ED上的其他地方运动时(点M与E，A，D三点不重合)，请直接写出∠BMC与∠ABM，∠DCM之间的数量关系.

【考点】

平行线的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知直线 $\text{[math]}$ 与直线 $\text{[math]}$ 分别交于 $\text{[math]}$ 两点， $\text{[math]}$ 和 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ，且 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ：

(2) 如图 2， $\text{[math]}$ 和 $\text{[math]}$ 的角平分线交于点 $\text{[math]}$ ，求 $\text{[math]}$ 的度数；

(3) 如图 3，若 $\text{[math]}$ ，延长线段 $\text{[math]}$ 得射线 $\text{[math]}$ ，延长线段 $\text{[math]}$ 得射线 $\text{[math]}$ ，射线 $\text{[math]}$ 绕点 $\text{[math]}$ 以每秒 $\text{[math]}$ 的速度逆时针旋转 $\text{[math]}$ 后停止，射线 $\text{[math]}$ 绕点 $\text{[math]}$ 以毎秒 $\text{[math]}$ 的速度顺时钋旋转 $\text{[math]}$ 以后停止. 设它们同时开始旋转，当射线 $\text{[math]}$ 时，求满足条件的t的值为多少.

综合题困难

2. 如图，已知DC∥FP，∠1=∠2，∠FED=28°，∠AGF=80°，FH平分∠EFG.

(1) 证明：DC∥AB；

(2) 求∠PFH的度数.

综合题普通

3. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F，∠1＝∠2．

(1) 试说明DG∥BC的理由；

(2) 如果∠B＝34°，且∠ACD＝47°，求∠3的度数．

综合题普通