1.
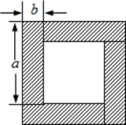
用几个小的长方形、正方形拼成一个大的正方形,然后利用两种不同的方法计算这个大的正方形的面积,可以得到一个等式 例如:计算图
例如:计算图 的面积,把图
的面积,把图 看作一个大正方形
看作一个大正方形 它的面积是
它的面积是 ;如果把图
;如果把图 看作是由
看作是由 个长方形和
个长方形和 个小正方形组成的,它的面积为
个小正方形组成的,它的面积为 , 由此得到
, 由此得到 .
.

(1)
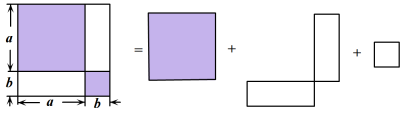
如图 , 由几个面积不等的小正方形和几个小长方形拼成一个边长为
, 由几个面积不等的小正方形和几个小长方形拼成一个边长为 的正方形,从中你能发现什么结论?该结论用等式表示为.
(2)
利用(1)中的结论解决以下问题:
(3)
如图
的正方形,从中你能发现什么结论?该结论用等式表示为.
(2)
利用(1)中的结论解决以下问题:
(3)
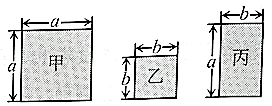
如图 , 正方形
, 正方形 边长为
边长为 , 正方形
, 正方形 边长为
边长为 , 点
, 点 ,
,  ,
,  在同一直线上,连接
在同一直线上,连接 、
、 , 若
, 若 ,
,  , 求图
, 求图 中阴影部分的面积.
中阴影部分的面积.
已知 ,
, 求
的值;
【考点】
完全平方公式的几何背景;
能力提升
真题演练