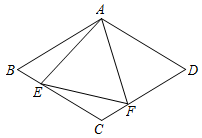
如图所示，在菱形ABCD中，，， △AEF为等边三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．

1. 如图所示，在菱形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， △AEF为等边三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．

(1) 证明不论E、F在BC、CD上如何滑动，总有 $\text{[math]}$ ；

(2) 当点E、F在BC、CD上滑动时，分别探讨四边形AECF和△CEF的面积是否发生变化？如果不变，求出这个定值；如果变化，求出最大（或最小）值．

【考点】

平行线的性质; 三角形的面积; 等边三角形的判定与性质; 菱形的性质; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 设一个三角形的三边分别为a ， b ， c ， p= $\text{[math]}$ （a+b+c），则有下列面积公式：S= $\text{[math]}$ （海伦公式）；S= $\text{[math]}$ （秦九韶公式）．

(1) 一个三角形的三边长依次为3，5，6，任选以上一个公式求这个三角形的面积；

(2) 一个三角形的三边长依次为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，任选以上一个公式求这个三角形的面积．

综合题普通

2. 如图所示，等边 $\text{[math]}$ 中，点D是 $\text{[math]}$ 的中点， $\text{[math]}$ 于点E， $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点F， $\text{[math]}$ .

求证：

(1) $\text{[math]}$ 是等边三角形；

(2) 求 $\text{[math]}$ 的周长.

综合题普通

3. 海伦—秦九韶公式：如果一个三角形三边长分别为a，b，c，设 $\text{[math]}$ ，则三角形的面积为 $\text{[math]}$ ，用公式计算下图三角形的面积.

综合题普通