正方形ABCD中，M为射线CD上一点（不与D重合），以CM为边，在正方形ABCD的异侧作正方形CFGM，连接BM、DF，直线BM与DF交于点E．

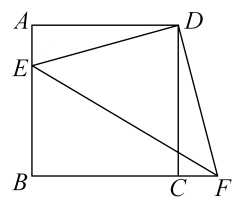
1. 正方形ABCD中，M为射线CD上一点（不与D重合），以CM为边，在正方形ABCD的异侧作正方形CFGM，连接BM、DF，直线BM与DF交于点E．

(1) 如图1，若M在CD的延长线上，求证：DF=BM，DF⊥BM；

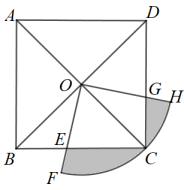
(2) 如图2，若M移到边CD上．

①在（1）中结论是否仍成立？（直接回答不需证明）

②连接BD，若BD=BF，且正方形CFGM边长为1，试求正方形ABCD的周长．

【考点】

正方形的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，点 $\text{[math]}$ 在正方形 $\text{[math]}$ 的边 $\text{[math]}$ 上，点 $\text{[math]}$ 在边 $\text{[math]}$ 的延长线上，且 $\text{[math]}$ ．求证：

(1) $\text{[math]}$ ；

(2) $\text{[math]}$ ．

综合题普通

2. 已知：四边形 $\text{[math]}$ 是正方形，E、F分别是 $\text{[math]}$ 和 $\text{[math]}$ 的延长线上的点，且 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 证明： $\text{[math]}$ .

综合题普通

3. 如图，正方形ABCD中，E是对角线BD上一点，连接AE，CE，延长AE交CD边于点F．

(1) 求证： $\text{[math]}$ ．

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ ．

综合题普通