1.
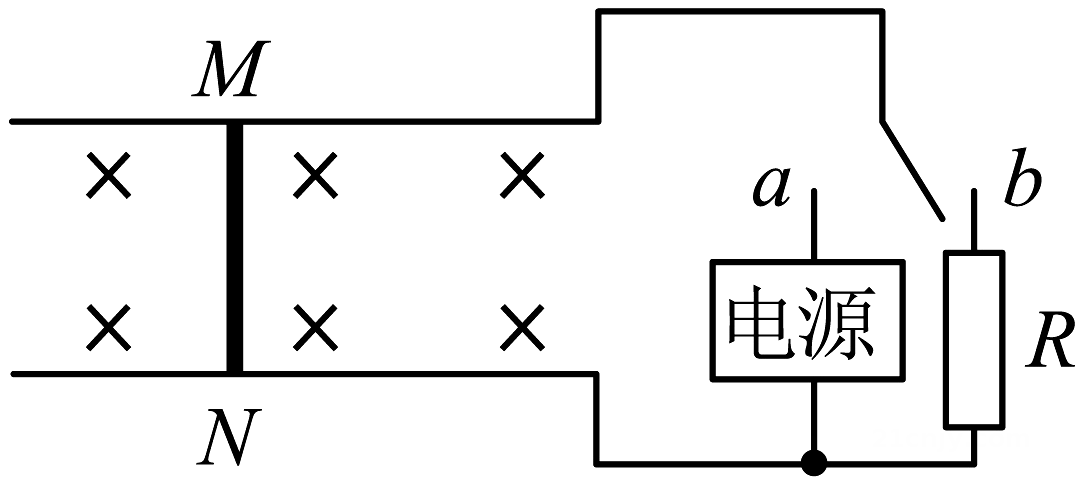
如图所示,间距L=1m的两平行光滑金属导轨,x轴平行导轨,y轴垂直导轨。在x=0位置左侧有一宽度为d=0.1m的光滑绝缘薄层(包括x=0处),隔开左右两部分电路。在导轨间存在磁场,y轴左侧磁场大小为B1=2T方向垂直纸面向外,y右侧磁场大小为B2 , 且满足B2=0.5x(T)变化,方向垂直纸面向外,在两轨道中x轴为坐标为x2=-0.5m的位置存在一个弹性装置,金属棒与弹性装置碰撞时瞬间等速弹回,导轨右侧的恒流源始终为电路提供恒定的电流I=8A(方向如图中箭头所示),导轨左侧接一阻值为R1=3Ω的电阻。阻值为R=1Ω质量为m=1kg的金属棒a垂直导轨静止于x=0处,与金属棒a完全相同的金属棒b垂直导轨静止于x1=0.5m处,金属棒a与金属棒b发生弹性碰撞。忽略一切阻力,已知弹簧振子周期公式 , 其中m为振子质量,k为回复力系数。求:
, 其中m为振子质量,k为回复力系数。求:

(1)
金属棒b第一次与金属棒a碰撞时的速度;
(2)
试定性画出金属棒a的I-t图像(对时间轴数值不做要求);
(3)
金属棒a最终停下位置和整个过程装置产生的焦耳热。
【考点】
电磁感应中的电路类问题;
电磁感应中的能量类问题;
能力提升