如图，已知射线BC⊥AB，以AB为斜边作Rt△ABD，延长AD到E，使得AD＝DE，连接BE，BF平分∠CBE交AE于点F．

1. 如图，已知射线BC⊥AB，以AB为斜边作Rt△ABD，延长AD到E，使得AD＝DE，连接BE，BF平分∠CBE交AE于点F．

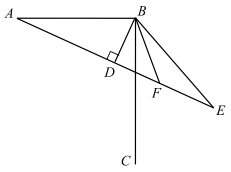
(1) 求证：BD＝DF；

(2) 若AB＝2，以AE为边向下作∠AEG＝45°，交射线BC于点G，求BG的长．

【考点】

三角形的外角性质; 线段垂直平分线的性质; 等腰三角形的性质; 角平分线的概念; 直角三角形斜边上的中线;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 问题：如图，在△ABD中，BA=BD，在BD的延长线上取点E，C，作△AEC，使EA=EC。若∠BAE=90°，∠B=45°，求∠DAC的度数。

答案：∠DAC=45°。

思考：

(1) 如果把以上“问题”中的条件“∠B=45°”去掉，其余条件不变，那么∠DAC的度数会改变吗？说明理由。

(2) 如果把以上“问题”中的条件“∠B=45°”去掉，再将“∠BAE=90°”改为“∠BAE=n°”，其余条件不变，求∠DAC的度数。

综合题普通

2. $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，AC的垂直平分线交AB于E，D为垂足，连结EC.

(1) 求 $\text{[math]}$ 的度数；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 长.

综合题普通

3. 将一根长为 $\text{[math]}$ 的铁丝，剪掉一部分后，剩下部分围成一个等腰三角形（接头部分忽略不计），这个等腰三角形的底为 $\text{[math]}$ ，腰为 $\text{[math]}$ ．

(1) 求剪掉部分的铁丝长度．

(2) 若围成的等腰三角形的周长为 $\text{[math]}$ ，求铁丝的长度．

综合题普通