1.
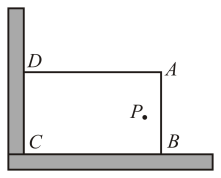
如图1,计划在长为30米、宽为20米的矩形地面上修筑两条同样宽的道路①、②(图中阴影部分),设道路①、②的宽为 米,剩余部分为绿化.
米,剩余部分为绿化.

(1)
道路①的面积为平方米;道路②的面积为平方米(都用含 的代数式表示).
(2)
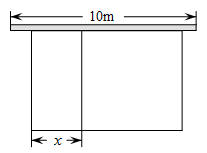
如图2,根据实际情况,将计划修筑的道路①、②改为同样宽的道路③(图中阴影部分),若道路的宽依然为
的代数式表示).
(2)
如图2,根据实际情况,将计划修筑的道路①、②改为同样宽的道路③(图中阴影部分),若道路的宽依然为 米,剩余部分为绿化,且绿化面积为551平方米,求道路的宽度.
米,剩余部分为绿化,且绿化面积为551平方米,求道路的宽度.
【考点】
一元二次方程的应用-几何问题;
能力提升
真题演练