1.
知识背景:我们在《全等三角形》一章中学习了全等三角形的性质和判定、等腰三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.

(1)
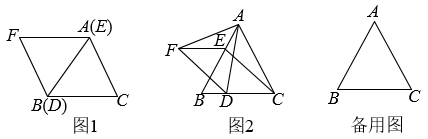
问题初探:如图 ,
,  中,
中, ,
,  , 点D是
, 点D是 上一点,连接
上一点,连接 , 以
, 以 为一边作
为一边作 , 使
, 使 ,
,  , 连接
, 连接 , 猜想
, 猜想 和
和 有怎样的数量关系,并说明理由.
(2)
方法迁移:如图
有怎样的数量关系,并说明理由.
(2)
方法迁移:如图 ,
,  是等边三角形,点D是
是等边三角形,点D是 上一点,连接
上一点,连接 , 以
, 以 为一边作等边三角形
为一边作等边三角形 , 连接
, 连接 , 则
, 则 、
、 、
、 之间有怎样的数量关系?
之间有怎样的数量关系? 直接写出答案,不写过程
直接写出答案,不写过程 (3)
类比再探:如图
(3)
类比再探:如图 ,
,  中,
中, ,
,  , 点M是
, 点M是 上一点,点D是
上一点,点D是 上一点,连接
上一点,连接 , 以
, 以 一边作
一边作 , 使
, 使 ,
,  , 连接
, 连接 , 则
, 则
 直接写出答案,不写过程,但要求作出辅助线
直接写出答案,不写过程,但要求作出辅助线 (4)
拓展创新:如图
(4)
拓展创新:如图 ,
,  是等边三角形,点M是
是等边三角形,点M是 上一点,点D是
上一点,点D是 上一点,连接
上一点,连接 , 以
, 以 为一边作等边三角形
为一边作等边三角形 , 连接
, 连接 , 猜想
, 猜想 的度数,并说明理由.
的度数,并说明理由.
【考点】
三角形全等的判定-SAS;
三角形的综合;
能力提升
真题演练