1.
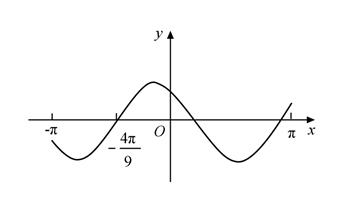
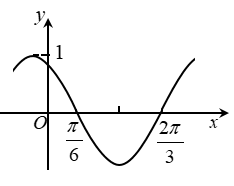
直线 都是函数
都是函数 的对称轴,且函数
的对称轴,且函数 在区间
在区间 上单调递增,则函数
上单调递增,则函数 的解析式为
的解析式为 .
.
【考点】
由y=Asin(ωx+φ)的部分图象确定其解析式;
能力提升
变式训练
拓展培优
真题演练