1.
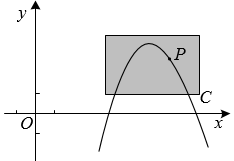
如图,点  在抛物线C:
在抛物线C:  上,且在C的对称轴右侧.
上,且在C的对称轴右侧.
(1)
写出C的对称轴和y的最大值,并求a的值;
(2)
坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为  ,
,  .平移该胶片,使
.平移该胶片,使  所在抛物线对应的函数恰为
所在抛物线对应的函数恰为  .求点
.求点  移动的最短路程.
移动的最短路程.
【考点】
二次函数图象的几何变换;
二次函数的最值;
平移的性质;
