1.
如图，在矩形ABCD中，点O是AB的中点，点M是射线DC上动点，点P在线段AM上（不与点A重合），OP= 
AB．
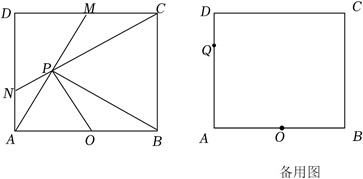
(1)
判断△ABP的形状，并说明理由．
(2)
当点M为边DC中点时，连接CP并延长交AD于点N．求证：PN=AN．
(3)
点Q在边AD上，AB=5，AD=4，DQ= 
，当∠CPQ=90°时，求DM的长．
【考点】
等腰三角形的性质;
相似三角形的判定与性质;
锐角三角函数的定义;
三角形全等的判定-SAS;
直角三角形斜边上的中线;
