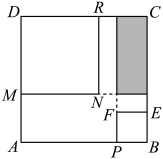
如图，四边形是证明勾股定理时用到的一个图形，，，是和边长，易知，这时我们把关于的形如的一元二次方程称为“勾系一元二次方程”. 请解决下列问题：

1. 如图，四边形 $\text{[math]}$ 是证明勾股定理时用到的一个图形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 和 $\text{[math]}$ 边长，易知 $\text{[math]}$ ，这时我们把关于 $\text{[math]}$ 的形如 $\text{[math]}$ 的一元二次方程称为“勾系一元二次方程”.

请解决下列问题：

(1) 写出一个“勾系一元二次方程”；

(2) 求证：关于 $\text{[math]}$ 的“勾系一元二次方程” $\text{[math]}$ 必有实数根；

(3) 若 $\text{[math]}$ 是“勾系一元二次方程” $\text{[math]}$ 的一个根，且四边形 $\text{[math]}$ 的周长是 $\text{[math]}$ ，求 $\text{[math]}$ 面积.

【考点】

完全平方公式及运用; 一元二次方程的根; 一元二次方程根的判别式及应用; 勾股定理的应用; 定义新运算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 阅读材料：

若x满足 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

解：设 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ，

∴ $\text{[math]}$ ，

∴ $\text{[math]}$ ．

类比应用：

(1) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的值．

(2) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

(3) 已知正方形 $\text{[math]}$ 的边长为a，点P和点R分别是边 $\text{[math]}$ 和 $\text{[math]}$ 上的点，且 $\text{[math]}$ ， $\text{[math]}$ ，分别以 $\text{[math]}$ 和 $\text{[math]}$ 为边长作正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ ．若图中阴影部分长方形的面积是4，则正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ 的面积和为．

综合题普通

2. 将完全平方公式 $\text{[math]}$ 进行适当的变形，可以解决很多的数学问题，例如，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.

解：因为 $\text{[math]}$ ，所以 $\text{[math]}$ ，即 $\text{[math]}$ .

又因为 $\text{[math]}$ ，所以 $\text{[math]}$ .

根据上面的解题思路与方法，解决下列问题.

(1) 若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ .

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的值.

(3) 如图，在长方形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点E、F是BC、CD上的点，且 $\text{[math]}$ ，分别以FC、CE为边在长方形 $\text{[math]}$ 外侧作正方形 $\text{[math]}$ 和 $\text{[math]}$ ，在长方形 $\text{[math]}$ 内侧作长方形 $\text{[math]}$ ，若长方形 $\text{[math]}$ 的面积为200，则图中阴影部分的面积和为.

综合题普通

3. 矩形纸片的长和宽分别为 $\text{[math]}$ 、 $\text{[math]}$ ，在纸片的四个角都剪去一个边长为 $\text{[math]}$ 的正方形.

(1) 请画出图形，并用含有 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的代数式表示纸片剩余部分的面积；

(2) 当 $\text{[math]}$ ，剩余部分的面积恰好等于剪去面积的4倍时，求纸片的长与宽.

综合题普通