1.
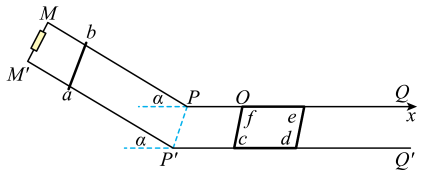
如图所示,MPQ、M′P′Q′是光滑平行导轨,其中倾斜部分MPP′M′为金属材料制成,电阻可不计,倾角为α=37°,并处在与MPP′M′平面垂直且向下的匀强磁场中(图中未画出),磁感应强度大小为2T;水平部分PQQ′P′为绝缘材料制成,所在空间内存在竖直方向的磁场,在PQ上取一点为坐标原点O,沿PQ方向建立x轴,可知磁感应强度分布规律为 (取竖直向上为正方向);两部分导轨的衔接处用小圆弧连接,金属棒通过时无机械能损失,两导轨间接有阻值为R=5Ω的定值电阻。正方形金属线框cdef的质量m2=2kg、边长为L=1m,每条边的电阻r2=2Ω,f点刚好位于坐标原点,fc边与PP′平行。现将一根质量m1=1kg,长度L=1m,电阻r1=2Ω的金属棒ab从图示位置静止释放,滑到斜面底端前已达到匀速运动。若整个过程ab棒、金属框与导轨始终接触良好,(重力加速度g=10m/s2 ,
(取竖直向上为正方向);两部分导轨的衔接处用小圆弧连接,金属棒通过时无机械能损失,两导轨间接有阻值为R=5Ω的定值电阻。正方形金属线框cdef的质量m2=2kg、边长为L=1m,每条边的电阻r2=2Ω,f点刚好位于坐标原点,fc边与PP′平行。现将一根质量m1=1kg,长度L=1m,电阻r1=2Ω的金属棒ab从图示位置静止释放,滑到斜面底端前已达到匀速运动。若整个过程ab棒、金属框与导轨始终接触良好,(重力加速度g=10m/s2 ,  ,
,  ),求:
),求:
(1)
ab棒滑到底端时的速度大小和ab棒两端的电压Uab;
(2)
ab棒与金属线框碰撞后合成一个整体一起在轨道上滑行,滑行过程中ed边产生的焦耳热;
(3)
第(2)所涉及的滑行过程中,通过ed棒的电荷量。
【考点】
动量守恒定律;
电流的概念;
电路动态分析;
法拉第电磁感应定律;
能力提升


