如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接AE，CD，AE与CD交于点M，AE与BC交于点N．

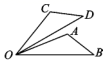
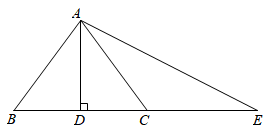
1. 如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接AE，CD，AE与CD交于点M，AE与BC交于点N．

(1) 求证：AE＝CD；

(2) 求证：AE⊥CD；

(3) 连接BM，有以下两个结论：①BM平分∠CBE；②MB平分∠AMD，其中正确的一个是（请写序号），并给出证明过程．

【考点】

三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

(1) 问题背景：
如图1：在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .E，F分别是 $\text{[math]}$ 上的点.且 $\text{[math]}$ .探究图中线段 $\text{[math]}$ 之间的数量关系.小王同学探究此问题的方法是，延长 $\text{[math]}$ 到点G.使 $\text{[math]}$ .连接 $\text{[math]}$ ，先证明 $\text{[math]}$ ，再证明 $\text{[math]}$ ，可得出结论，他的结论应是.

(2) 探索延伸：
如图2，若在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .E，F分别是 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，上述结论是否仍然成立，并说明理由.

综合题困难

(1) 如图①，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 上的点，且 $\text{[math]}$ ．请直接写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系：；

(2) 如图②，在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 上的点，且 $\text{[math]}$ ，（1）中的结论是否仍然成立？请写出证明过程；

(3) 在四边形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 分别是边 $\text{[math]}$ ， $\text{[math]}$ 所在直线上的点，且 $\text{[math]}$ ．请画出图形（除图②外），并直接写出线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 之间的数量关系．

综合题困难

3. 如图， $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上， $\text{[math]}$ .

(1) 如图1，若点 $\text{[math]}$ 在线段 $\text{[math]}$ 上，判断 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系和位置关系，并说明理由；

(2) 如图2，若点 $\text{[math]}$ 在线段 $\text{[math]}$ 的延长线上，其他条件不变，试判断（1）中结论是否成立，并说明理由.

综合题普通