如图，在平面直角坐标系中，点A(-4，0)，C(3，0)，D(0，4)， AG⊥CD于点G，交y轴于点B.

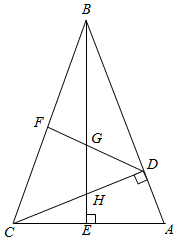
1. 如图，在平面直角坐标系中，点A(-4，0)，C(3，0)，D(0，4)， AG⊥CD于点G，交y轴于点B.

(1) 求证：△AOB≌△DOC．

(2) 点E在线段AB上，作OF⊥OE交CD于点F，连结EF．

①若E是AB的中点，求△OEF的面积.

②连结DE，当△DEF是以DE为腰的等腰三角形时，求CF的长．

【考点】

三角形的面积; 角平分线的性质; 勾股定理; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在 $\text{[math]}$ ABC中，∠ABC＝45°，CD⊥AB，BE⊥AC，垂足分别为D，E，F为BC中点，BE与DF、DC分别交于点G，H，∠ABE＝∠CBE．

(1) 线段BH与AC相等吗？若相等给予证明，若不相等请说明理由；

(2) 求证：BG²﹣GE²＝EA²；

(3) 若BC＝2 $\text{[math]}$ ，求 $\text{[math]}$ BDH的面积．

综合题普通

2. 如图，射线 $\text{[math]}$ 于点A、点C、B在 $\text{[math]}$ 、 $\text{[math]}$ 上，D为线段 $\text{[math]}$ 的中点，且 $\text{[math]}$ 于点E.

(1) 若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ 的周长为24，求 $\text{[math]}$ 的面积；

(3) 若 $\text{[math]}$ ，C点在射线 $\text{[math]}$ 上移动，问此过程中， $\text{[math]}$ 的值是否为定值？若是，请求出这个定值；若不是，请求出它的取值范围.

综合题普通

3. 如图，在△ABC中，AB=AC，∠ABC=72°．

(1) 用直尺和圆规作∠ABC的平分线BD交AC于点D（保留作图痕迹，不要求写作法）；

(2) 在（1）中作出∠ABC的平分线BD后，求∠BDC的度数．

综合题普通