如图，四边形ABCD中，∠B＝∠C＝90°，点E为BC中点，AE⊥DE于点E.点O是线段AE上的点，以点O为圆心，OE为半径的⊙O与AB相切于点G，交BC于点F，连接OG.

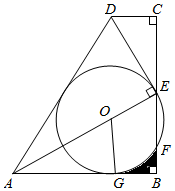
1. 如图，四边形ABCD中，∠B＝∠C＝90°，点E为BC中点，AE⊥DE于点E.点O是线段AE上的点，以点O为圆心，OE为半径的⊙O与AB相切于点G，交BC于点F，连接OG.

(1) 求证：△ECD∽△ABE；

(2) 求证：⊙O与AD相切；

(3) 若BC＝6，AB＝3 $\text{[math]}$ ，求⊙O的半径和阴影部分的面积.

【考点】

勾股定理; 切线的判定; 扇形面积的计算; 相似三角形的判定; 几何图形的面积计算-割补法;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

综合题普通

综合题普通

3. 如图， $\text{[math]}$ 中， $\text{[math]}$ ，点O在边 $\text{[math]}$ 上，以点O为圆心， $\text{[math]}$ 为半径的 $\text{[math]}$ 交 $\text{[math]}$ 于D，交 $\text{[math]}$ 于E，若 $\text{[math]}$ ．

综合题普通