1.
学习了图形的旋转之后,小明知道,将点  绕着某定点
绕着某定点  顺时针旋转一定的角度
顺时针旋转一定的角度  ,能得到一个新的点
,能得到一个新的点  .经过进一步探究,小明发现,当上述点
.经过进一步探究,小明发现,当上述点  在某函数图象上运动时,点
在某函数图象上运动时,点  也随之运动,并且点
也随之运动,并且点  的运动轨迹能形成一个新的图形.
的运动轨迹能形成一个新的图形.
试根据下列各题中所给的定点 的坐标和角度
的大小来解决相关问题.
(1)
(初步感知)
(2)
若点  的运动轨迹经过点
的运动轨迹经过点  ,求原一次函数的表达式.
(3)
(深入感悟)
(4)
(灵活运用)
,求原一次函数的表达式.
(3)
(深入感悟)
(4)
(灵活运用)
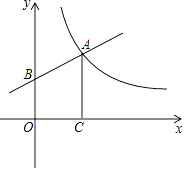
如图1,设 ,
,点
是一次函数
图像上的动点,已知该一次函数的图象经过点
.
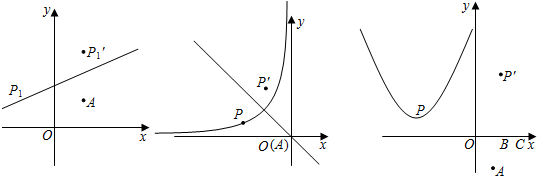
点 旋转后,得到的点
的坐标为;
如图2,设 ,
,点
反比例函数
的图像上的动点,过点
作二、四象限角平分线的垂线,垂足为
,求
的面积.
如图3,设A ,
,点
是二次函数
图像上的动点,已知点
、
,试探究
的面积是否有最小值?若有,求出该最小值;若没有,请说明理由.
【考点】
待定系数法求一次函数解析式;
反比例函数系数k的几何意义;
三角形全等的判定;
旋转的性质;
二次函数与一次函数的综合应用;