1.
为了防控新冠疫情，某地区积极推广疫苗接种工作，卫生防疫部门对该地区八周以来的相关数据进行收集整理，绘制得到如下图表：
该地区每周接种疫苗人数统计表
|
周次 |
第1周 |
第2周 |
第3周 |
第4周 |
第5周 |
第6周 |
第7周 |
第8周 |
|
接种人数（万人） |
7 |
10 |
12 |
18 |
25 |
29 |
37 |
42 |
|
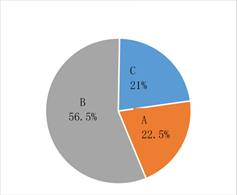
该地区全民接种疫苗情况扇形统计图 | A：建议接种疫苗已接种人群 B：建议接种疫苗尚未接种人群 C：暂不建议接种疫苗人群 | |||||||
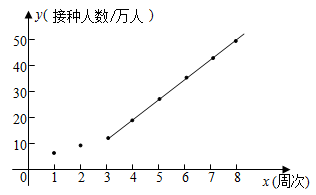
根据统计表中的数据，建立以周次为横坐标，接种人数为纵坐标的平面直角坐标系，并根据以上统计表中的数据描出对应的点，发现从第3周开始这些点大致分布在一条直线附近，现过其中两点 、
作一条直线（如图所示，该直线的函数表达式为
），那么这条直线可近似反映该地区接种人数的变化趋势.
请根据以上信息，解答下列问题：
(1)
这八周中每周接种人数的平均数为万人：该地区的总人口约为万人；
(2)
若从第9周开始，每周的接种人数仍符合上述变化趋势.
(3)
实际上，受疫苗供应等客观因素，从第9周开始接种人数将会逐周减少 
万人，为了尽快提高接种率，一旦周接种人数低于20万人时，卫生防疫部门将会采取措施，使得之后每周的接种能力一直维持在20万人.如果 
，那么该地区的建议接种人群最早将于第几周全部完成接种？
①估计第9周的接种人数约为 ▲ 万人；
②专家表示：疫苗接种率至少达60%，才能实现全民免疫.那么，从推广疫苗接种工作开始，最早到第几周，该地区可达到实现全民免疫的标准？
【考点】
一元一次不等式的应用;
一次函数的实际应用;
用样本估计总体;
平均数及其计算;
能力提升