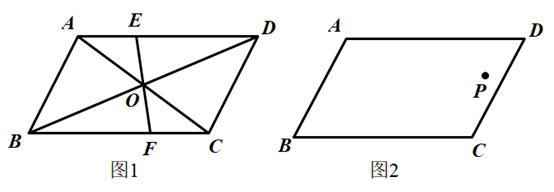
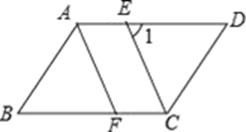
如图，在正方形ABCD中，AB=2，连接AC。P，Q两点分别从A，D同时出发，点P以每秒1个单位长度的速度沿线段AB向终点B运动；点Q沿折线D→A→C向终点C运动，在DA上的速度为每秒2个单位长度，在AC上的速度为每秒2 个单位长度。在运动过程中，以AP，AQ为邻边作平行四边形APMQ。设运动时间为x秒，平行四边形APMQ和正方形ABCD重叠部分的图形面积为y。

1. 如图，在正方形ABCD中，AB=2，连接AC。P，Q两点分别从A，D同时出发，点P以每秒1个单位长度的速度沿线段AB向终点B运动；点Q沿折线D→A→C向终点C运动，在DA上的速度为每秒2个单位长度，在AC上的速度为每秒2 $\text{[math]}$ 个单位长度。在运动过程中，以AP，AQ为邻边作平行四边形APMQ。设运动时间为x秒，平行四边形APMQ和正方形ABCD重叠部分的图形面积为y。

(1) 当点M在BC上时，x=

(2) 求y关于x的函数解析式，并写出x的取值范围；

(3) 连接MB，当0°<∠MBP<90°时，直接写出tan∠MBP= $\text{[math]}$ 时x的值。

【考点】

平行四边形的性质; 正方形的性质; 相似三角形的判定与性质; 锐角三角函数的定义; 一次函数中的动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在平行四边形 $\text{[math]}$ 中， $\text{[math]}$ ．

(1) 在 $\text{[math]}$ 边上确定点 $\text{[math]}$ ，使点 $\text{[math]}$ 到边 $\text{[math]}$ ， $\text{[math]}$ 的距离相等（用尺规作图，不写作法，保留作图痕迹）；

(2) 在（1）中所作的图形中，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ ．

综合题普通

2. 如图1，ABCD是平行四边形对角线AC，BD相交于点O，直线EF过点O，分别交AD，BC于点E，F．

(1) 求证：AE=CF．

(2) 如图2，若ABCD是老张家的一块平行四边形田地。P为水井，现要把这块田地平均分给两个儿子，为了用水方便，要求分给两个儿子的田地都与水井P相邻。请你帮老张家设计一下，画出图形，并说明理由？

综合题普通

3. 如图，在▱ABCD中，CE平分∠BCD，且交AD于点E，AF∥CE，且交BC于点F.

(1) 求证：△ABF≌△CDE；

(2) 如图，若∠B=52°，求∠1的大小.

综合题普通