1.
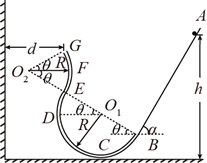
如图所示，竖直平面内由倾角α=60°的斜面轨道AB、半径均为R的半圆形细圆管轨道BCDE和圆周细圆管轨道EFG构成一游戏装置固定于地面，B、E两处轨道平滑连接，轨道所在平面与竖直墙面垂直。轨道出口处G和圆心O2的连线，以及O2、E、O1和B等四点连成的直线与水平线间的夹角均为θ=30°，G点与竖直墙面的距离 
。现将质量为m的小球从斜面的某高度h处静止释放。小球只有与竖直墙面间的碰撞可视为弹性碰撞，不计小球大小和所受阻力。
(1)
若释放处高度h=h0 ， 当小球第一次运动到圆管最低点C时，求速度大小vc及在此过程中所受合力的冲量的大小和方向；
(2)
求小球在圆管内与圆心O1点等高的D点所受弹力FN与h的关系式；
(3)
若小球释放后能从原路返回到出发点，高度h应该满足什么条件？
【考点】
动量定理;
牛顿第二定律;
平抛运动;
机械能守恒定律;