0 返回首页
1. 如图，在 中，∠B=25°，∠BAC=31°，过点A作BC边上的高，交BC的延长线于点D ， CE平分∠ACD ， 交AD于点E ．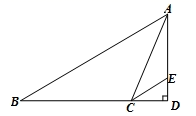

求：

(1) ∠ACD的度数；
(2) ∠AEC的度数．
【考点】
三角形的外角性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 对于下列问题，在解答过程的空白处填上适当的内容（理由或数学式）．

如图，在直角△ABC中，CD是斜边AB上的高，∠BCD＝35°．

(1) 求∠EBC的度数；

解：∵CD⊥AB（已知），

∴∠CDB＝      ▲            °．

∵∠EBC＝∠CDB+∠BCD（    ）．

∴∠EBC＝      ▲            °+35°＝      ▲            °（等量代换）．
(2) 求∠A的度数．
∵∠EBC＝∠A+∠ACB（    ），

∴∠A＝∠EBC-∠ACB（等式的性质）．

∵∠ACB＝90°（已知），

∴∠A＝            ▲            -90°＝      ▲            °（等量代换）．
综合题 普通
2. 中， ，点D、E分别是 边 上的两个定点，点Р是平面内一动点，记 ， .

 

(1) 初探：
如图1，若点P在线段 上运动，

①当 时，则 °；

② 之间的关系为：.
(2) 再探：
若点Р运动到边 的延长线上，如图2，则 之间有何关系?并说明理
(3) 拓展：
如图3，写出此时 之间的关系，并说明理由.
综合题 普通
3. （概念认识）

如图①，在∠ABC中，若∠ABD＝∠DBE＝∠EBC，则BD，BE叫做∠ABC的“三分线”.其中，BD是“邻AB三分线”，BE是“邻BC三分线”.

 

(1) （问题解决）如图②，在△ABC中，∠A＝70°，∠B＝45°，若∠B的三分线BD交AC于点D，则∠BDC＝°；
(2) 如图③，在△ABC中，BP、CP分别是∠ABC邻AB三分线和∠ACB邻AC三分线，且BP⊥CP，求∠A的度数；
(3) （延伸推广）在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P.若∠A＝m°，∠B＝n°，直接写出∠BPC的度数.（用含 m、n的代数式表示）
综合题 普通