1.
在平面直角坐标系xOy中，函数F1和F2的图象关于y轴对称，它们与直线x=t(t>0)分别相交于点P，Q。
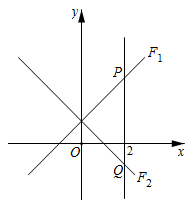
(1)
如图，函数F1为y=x+1，当t=2时，PQ的长为；
(2)
函数F1为y= 
，当PQ=6时，t的值为 ；
(3)
函数F1为y=ax2+bx+c (a≠0)，
①当t= 时，求△OPQ的面积；
②若c>0，函数F1和F2的图象与x轴正半轴分别交于点A(5，0)，B(1，0)，当c≤x≤c+1时，设函数F1的最大值和函数F2的最小值的差为h，求h关于c的函数解析式，并直接写出自变量c的取值范围。
【考点】
二次函数的最值;
三角形的面积;
关于坐标轴对称的点的坐标特征;