1.
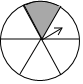
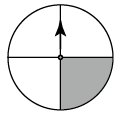
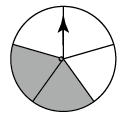
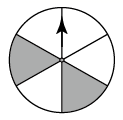
四张背面完全相同的卡片,正面分别印有等腰三角形、圆、平行四边形、正六边形,现在把它们的正面向下,随机的摆放在桌面上,从中任意抽出一张,则抽到的卡片正面是中心对称图形的概率是( )
A.
 B.
B.
 C.
C.
 D.
1
D.
1
【考点】
几何概率;
概率的简单应用;
基础巩固
能力提升
变式训练
拓展培优